If you came here for the code and a live demo here it is! If you came here to learn about cellular automata and why I find it incredibly fascinating, read on.
Conway’s Game of Life

There are many types of cellular automata but Life holds a special place in my heart. Four simple rules give rise to beautiful complexity:
- Any live cell with fewer than two live neighbors dies as if caused by underpopulation.
- Any live cell with two or three live neighbors lives on to the next generation.
- Any live cell with more than three live neighbors dies as if by overpopulation.
- Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
Through each step in time, each of the rules is evaluated simultaneously for each cell. This means the outcome is entirely deterministic. Give two people in different rooms the same seed generation and they will always end up with the same end result. I find this incredible. It is almost like the epic saga of human civilization is compressed in a single image.
This is also why hashing is useful. Given any initial state, you always produce the same end state. But it’s a one-way street! Given only the end state, you cannot walk it back to the initial state (unless you have a rainbow table, but that’s a whole separate topic).
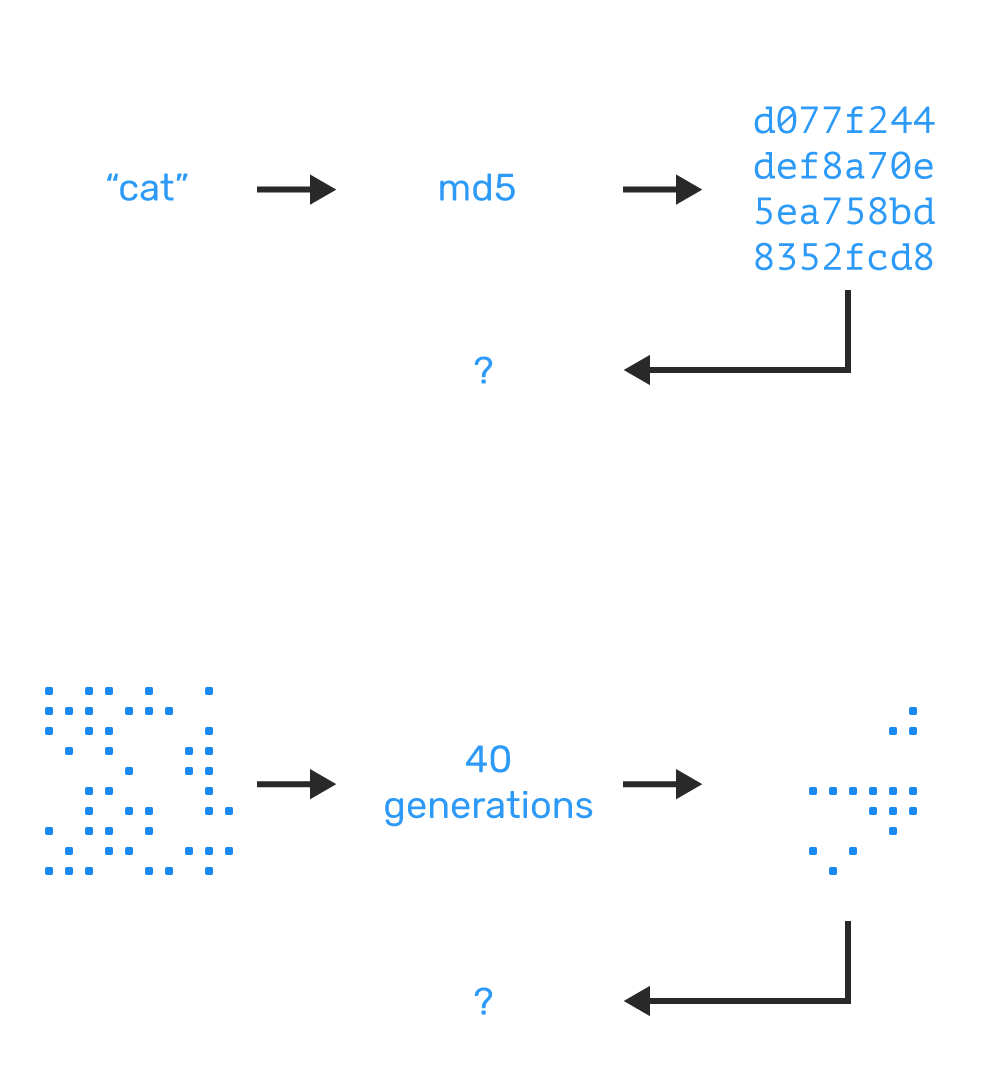
Unlike cryptography, the practical utility of cellular automata is limited… but the artistic utility is not!
Algorithmic Art
Algorithmic art has always fascinated me because it allows for emergence. Small units organizing into larger patterns is resonant with so many human experiences: family structures, music performances, food, traffic patterns, crowd behavior... Some of my favorite artists who incorporate emergence and algorithms into their practices:
- Antonio Roberts (live visual performances, installations)
- Julian Oliver (all of his work is incredible and provocative; one of my favorites is “A ceremonial automaton for the Sixth Mass Extinction”)
- Mark Beasley (Chicago new-media artist)
- Rosa Menkman (“[her] work focuses on noise artifacts that result from accidents in both analog and digital media such as glitch, encoding and feedback artifacts”)
- Autechre (the de facto pioneers in algorithmic music composition with Max)
- Brian Eno (77 Million Paintings, Bloom, Ambient 1)
- There are even events and collectives like Algorithmic Art Assembly and Algorave.
The JavaScript Implementation
Inspired by these artists, I developed my own JavaScript implementation of Conway’s Game of Life. I wanted to do it in pure JS (no jQuery or anything like that) and keep it time-boxed to just a couple hours of development. This latter point was important to me because this is the type of project that an artist or scientist could base their entire practice around!
I actually ended up programming this chronologically last, but I had a rough vision first:
It’s the four rules of Conway’s Game of Life! And simple, one-line, pure logic functions like these bring me joy. As we can see, each rule only cares about the count of the cell’s neighbors. This is great news from an interface perspective.
Next up is our grid. I decided to make the grid size configurable. No matter what values you choose for x and y, the cartesian position “0,0” maps to the south-east corner and the max value of “x,y” maps to the north-west corner. I could make an argument for making any corner “0,0” and this one made the most sense to me given how JS likes to iterate.
Each cell on the grid has a unique class assigned to it. Yes, class. Not ID. At Highland, we always use classes.
Now that we know our coordinate system so we can write some functions to handle the census:
isLive(x, y) accepts the x and y coordinates of a cell and tells you if that cell is alive or dead via an HTML5 data attribute. This is the function does a lot of work for us in the next two functions.
getNeighbors(x, y) also accepts the x and y coordinates of a cell. This function returns the count of living neighbors. This function is a little long and verbose for my tastes but I value the clarity of having one line for each north, south, east, west permutation. I tried refactoring this a few times but I found it too diluted to understand.
Finally census(x, y) tells us the fate of our cell in question.
The rest is just boring DOM manipulation, initial randomization, and re-seed stuff. The last portion of note is how I handled the current and future grids:
The current grid of life is built out in the.life div programmatically based on the x and y size as defined in the config object. As the program steps through time the new state is built the hidden .next div before being copied over to .life. Think of it as a little DOM buffer.
Conclusion
This was a fun way to spend a Saturday morning. Future lines of inquiry are centering around translating this to music somehow.
I’m also curious about experimenting with different rules of life. What would happen if you redefined the overpopulation threshold? Reversed the operators? Added a new rule?



